An argument often made for the existence of “g” is that it is the so called “active ingredient” of the IQ tests predictive power. The argument can be summarized as such: Controlling for ‘g’, the subscores, or item scores of the IQ test no longer predicts important outcomes like grades, income, SES and so on. In other words, subscores have no incremental validity. I/O psychologists have even a made catchphrase for this finding: “Not much more than g”
It is not my intention to review the whole literature in this post, but to go over the conceptual issues with studies test this hypothesis, and why they are not as strong as they may seem at first glance.
1st: The (factor)structure of most IQ tests
I use term “factors” here loosely, will elaborate in a later post
I also use the term “narrow” and “broad” as levels of generality in this example, not using the CHC conviction
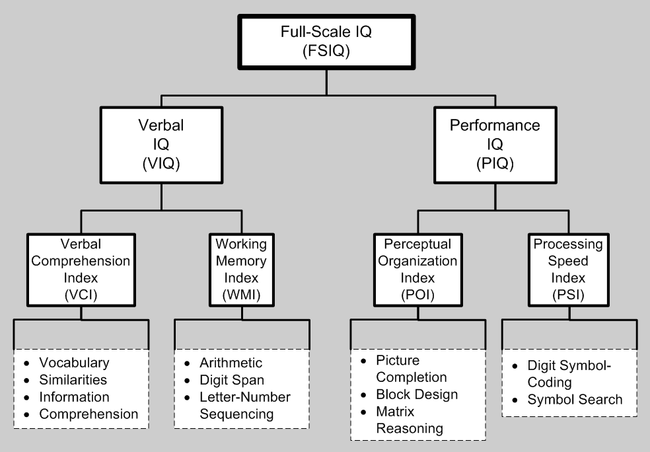
In the picture, you can see the structure of the WAIS-III. The actual names of the factors are not important. We only need to know that FSIQ(a proxy for g) is at the top, while other so called broad factors are below it, and below the broad factors there are the so called narrow factors. The narrow factors are measured by the subtests at the bottom of the picture. The broad factors, and g are actually not measured at all, they are extracted by running a fairly sophisticated statistical procedure called factor analysis(more on this in a later post). When it comes to individual administration the scores for broad factors and FSIQ are usually calculated by a weighted sum of the subtest, but other methods are possible too.
Note two things:First, in this example, there are 7 scores to be computed, while there are only 12 subtests. Second, the FSIQ(g) is effectively calculated by using the scores from all the subtests, while broad factors are calculated only by using the subtests that are below said factors. The narrow abilities use even less subtests. The implication of these facts is clear: Measurement error is much higher at the broad and narrow factor level than at the general factor level. As we know, measurement error deflates the “true” correlation between the predictor and the outcome. Even at the latent variable level, the measurement of the broad factors is questionable. ( Dombrowski et al 2015 )
2nd: Assumptions of causality
“Intentionally or not, when researchers use incremental validity analysis to evaluate a specific aptitude theory, they invoke the assumption that an underlying latent trait (i.e., GMA) accounts for the variance shared across test scores. Lang et al. have noted this view is theoretically close (although not identical) to Spearman’s original idea that all variance that tests in a battery share is attributable to the general factor… The idea that the variance shared by GMA and narrower cognitive abilities is attributable to GMA is also theoretically in line with higher-order conceptualizations of intelligence. In these conceptualizations, GMA is the underlying source of shared variance between the narrower cognitive abilities. Despite the prevalence of the practice, it is important for researchers and practitioners to realize that entering GMA first in incremental validity analysis is a choice—and not one they need to feel compelled to make.”(Kell & Lang 2017)
Simply stated, all of these studies assume that g causes the broad factors. By controlling for g, researchers also indirectly control for parts of the broad ability too! This makes sense if we think g is causal, however many emergent theories do not regard g as a reflective variable. Notable mentions include: Dynamic Mutualism, POT, and the PASS theory of intelligence.
Kell and Lang illustrates that depending on our theoretical assumptions, we can get quite different results from the same data.
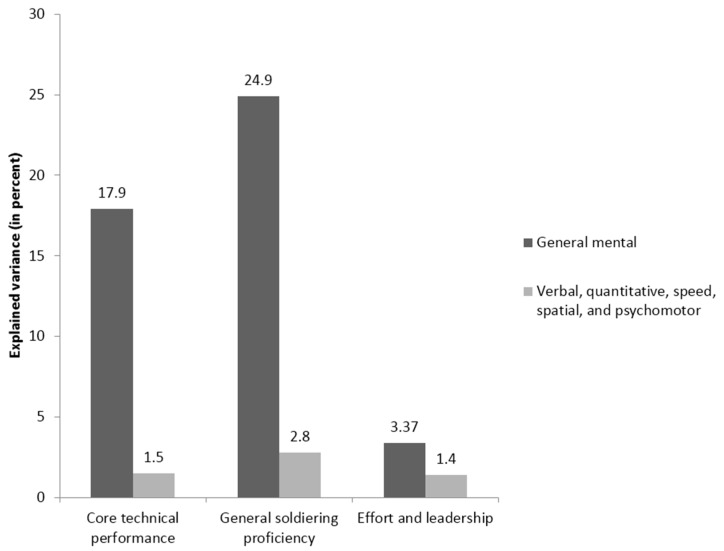Here we can see the traditional “incremental validity” approach
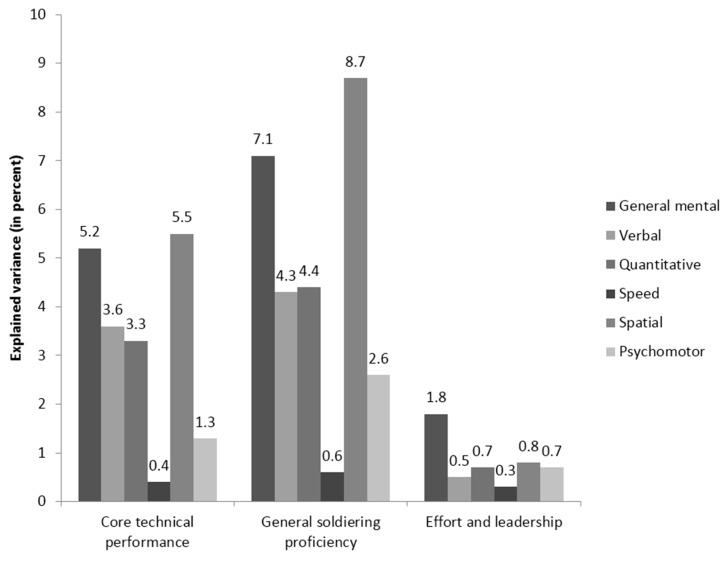And here is depicted the “relative importance analysis” approach. As is evident, the results vary significantly. I do not wish to advocate for either approach here. Ultimately, we do not yet fully comprehend what g represents.
Lastly, there is strong emerging evidence for the existence of more than g using the traditional incremental validity approach.
The final counterargument against the “not much more than g” assertion comes from (Coyle et al 2008). It is well-known that the SAT and ACT are g-loaded tests and that they somewhat predict academic outcomes. It is also acknowledged that g predicts academic outcomes. Some researchers speculated that the predictive validities of the SAT/ACT were exclusively due to g. Coyle and Pillow tested whether these tests predict outcomes after statistically removing g. Surprisingly, the residuals(u13 in the pictures) predicted grades just as well as g does! This is noteworthy, especially considering that if we assume a g-loading of about 0.8 is accurate, then g explains approximately 64% of the variance in the SAT/ACT scores. These results have been replicated in Coyle et al’s other works.
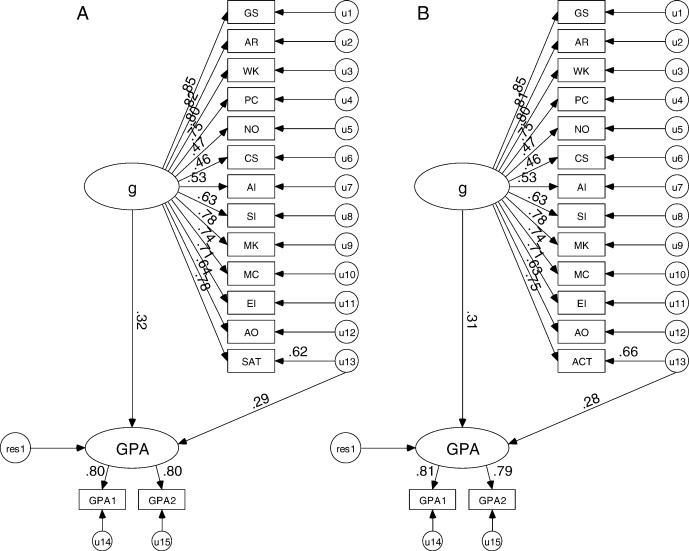
Conclusion: The usual incremental validity approach has its doubts, and even with this method, newer studies suggest there’s more to it than just “g”.